In grafica 3D movimenti, rotazioni, ridimensionamenti sono comunemente chiamati trasformazioni affini. Trasformare un solido significa eseguire delle operazioni su ogni vertice in modo che il poligoni vengano posizionati in modo corretto. L'operazione da applicare è un prodotto di ogni singolo punto per una struttura chiamata matrice.

Una matrice è una tabella di numeri reali di dimensione NxM.

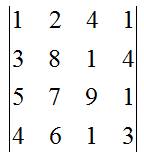
I valori al suo interno vengono chiamati elementi della matrice e si identificano citando il numero della riga orizzontale partendo dall’alto e della colonna verticale partendo da sinistra.

In DirectX10 una matrice composta da 4 righe e 4 colonne è rappresentata dalla struttura

D3DXMATRIX matrix;

Questo è il tipo che si utilizzerà in computer grafica.

La somma di due matrici equivale ad una matrice i cui elementi sono la somma degli elementi dei due addendi presi uno per uno. Ad esempio

La somma, come per le operazioni tradizionali gode della proprietà commutativa, associativa e distributiva. L’elemento neutro per la somma è la matrice nulla composta da elementi tutti uguali a zero.

Il prodotto tra matrice è invece una operazione particolare chiamata prodotto riga per colonna. Il procedimento consiste nel prendere ogni riga della prima matrice e fare un prodotto vettoriale con tutte le colonne della seconda. Il risultato si andrà a posizionare nell’elemento di riga e colonna utilizzate.

Il prodotto è possibile solo se il numero degli elementi presenti nella riga della prima matrice è uguale a quello delle colonne della seconda.

Il prodotto tra matrici non gode di proprietà commutativa. Moltiplicare M1 per M2 produrrà nella maggior parte dei casi un risultato diverso da M1 per M2. L’unica eccezione è per l’elemento neutro rispetto alla moltiplicazione che si definisce matrice identità.

La matrice identità è una matrice composta da tutti zero eccetto la diagonale dalla posizione in alto a sinistra a quella in basso a destra che contiene il valore uno.

La matrice identità equivale all’uno nella moltiplicazione ed in questo caso produce sempre lo stesso risultato, sia se moltiplicata a destra che a sinistra.

Per ottenere la matrice identità si utilizza l’istruzione

D3DXMatrixIdentity(&matrix);

il prodotto e la moltiplicazione si possono effettuare in modo tradizionale con gli operatori + e * (quest’ultimo può essere anche utilizzato con l’istruzione D3DXMatrixMultiply).

Le matrici sono utilizzate in computer grafica per contenere informazioni sulla posizione, rotazione e proporzione di un oggetto. Trasformare un oggetto significa moltiplicare ogni vertice per opportune matrici.

Le trasformazioni primitive con le matrici sono la traslazione, la rotazione e la scala. Moltiplicando tra loro varie matrici primitive è possibile ottenere trasformazioni complesse.

La cosa più interessante è che si moltiplica per quel vertice il prodotto di una matrice di traslazione con una di rotazione i due movimenti verranno inseriti in sequenza ma attenzione all'ordine:
TRASLARE e RUOTARE è DIFFERENTE DA RUOTARE E TRASLARE, guardate sotto.

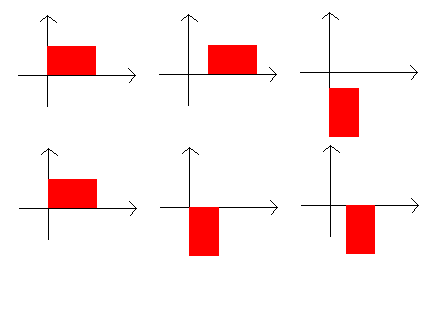
In alto ho applicato prima una traslazione a destra e poi una rotazione di 90° in senso orario. Sotto ho invece applicato prima la rotazione e poi la traslazione e come potete vedere la situazione è diversa. Questo perché le trasformazioni vengono sempre fatte considerando come centro l'origine degli assi e perché il prodotto di matrici non è commutativo. Ogni movimento sarà quindi una concatenazione di movimenti semplici ottenuti moltiplicando tra di loro più matrici primitive secondo un preciso ordine.

In DirectX10 le matrici primitive si ottengono con queste istruzioni

Traslazione

D3DXMatrixTranslation (&matrix, X, Y, Z);

Crea una matrice traslata dei valori X, Y, Z;

Rotazione

D3DXMatrixRotationX (&matrix, angle);

D3DXMatrixRotationY (&matrix, angle);

D3DXMatrixRotationZ (&matrix, angle);

Sono di 3 tipi, a seconda dell’asse su cui si vuole ruotare. L’angolo è espresso in radianti (per convertire da gradi a radianti bisogna moltiplicare per (3.14/180).

Scala

D3DXMatrixScaling (&matrix, X,Y,Z);

Effettua un ridimensionamento lungo l’asse. Valori superiori ad 1 aumentano la dimensione (esempio 2 è il doppio, 3 il triplo), valori inferiori ad 1 invece diminuiscono (0,5 è la metà, 0,3333 è un terzo)

Compreso il funzionamento delle matrici di trasformazione è necessario introdurre il concetto di vista e proiezione. Una scena tridimensionale consiste nel posizionamento di tanti oggetti che, tramite le matrici di trasformazione, si dispongono in una scena. Gli oggetti passeranno dalla posizione che avevano al momento della loro creazione a quella definitiva nella scena. Ciò non è però sufficiente per rappresentare una scena nel nostro monitor. Manca un punto importante, da dove la scena viene guardata. Il paragone più semplice è quello della telecamera che inquadra la scena da una certa posizione. Per fare questo si utilizza di nuovo una matrice chiamata View. La view matrix applicata ad un oggetto a cui è stata applicata una world matrix fa in modo che l’oggetto venga posizionato rispetto alla telecamera. L’oggetto inquadrato si troverà al centro della scena, quelli non inquadrati al lato fino ad uscire dalla visuale. La matrice view viene costruita utilizzando 3 informazioni:

1. ViewAt: banalmente la posizione della telecamera
2. ViewTo: il punto verso cui la telecamera guarda
3. ViewUp: l’angolo della telecamera intorno alla direzione in cui guarda

Tramite le prime due viene calcolato cosa si guarda mentre con la terza l’angolo con cui la scena è vista (ad esempio si può ruotare la telecamera inquadrando il mondo sottosopra o inclinato).

Terminata questa trasformazione che viene chiamata “portare l’oggetto in View Space”, avremo al centro dello schermo gli oggetti allineati alla camera e ai lati quelli distanti. Gli assi cartesiani saranno allineati allo schermo con X ed Y corrispondenti alla direzione orizzontale e verticale del monitor, e la Z perpendicolare al monitor. Esistono 2 modi di considerare la Z, il sistema sinistrorso e destrorso (left-handed e right-handed). In uno la Z aumenta in direzione del monitor, nell’altro quando esce dal monitor.

Per creare la matrice view si utilizzano una di queste istruzioni a seconda del tipo di coordinate.

D3DXMatrixLookAtLH(&view,&viewAt,&viewTo,&viewUp);

D3DXMatrixLookAtRH(&view,&viewAt,&viewTo,&viewUp);

Dove viewAt, viewTo e viewUp sono strutture D3DXVECTOR3 che contengono 3 float, X, Y e Z.

Terminato questo manca l’ultimo passaggio.

La scena dopo la World e la View è ancora misurabile nell’unità di misura 3D mentre i nostri schermi sono bidimensionali. La scena da tre dimensione deve subire una operazione di “proiezione” che porta l’oggetto su un piano. In DirectX, la dimensione dello schermo ha come forma un quadrato di lato 2 con l’angolo in basso a sinistra uguale a -1,-1 e quello in alto a destra 1,1. Per quest’ultima operazione si usa la Projection Matrix. Esistono diversi tipi di proiezione, le più importanti sono la proiezione prospettica e quella ortogonale. La prima è quella che corrisponde ai nostri occhi: gli oggetti ci appaiono più grandi quando vicini e sempre più piccoli quando si allontanano permettendoci una visuale molto più grande in lontananza. La proiezione ortogonale invece mantiene inalterate le dimensioni lungo la distanza. Per semplificare il concetto prendiamo come esempio 2 cubi di uguale dimensione posti uno dietro l’altro a distanza differenti e guardiamoli in modo da allinearci ad essi. Nella prospettiva il cubo dietro ci apparirà più piccolo mentre nella proiezione ortogonale saranno perfettamente uguali, anche a distanze lontanissime. Questa forma è molto utile per lavori di tecnica mentre la prospettiva è più comune rappresentando il comportamento normale della vista.

Ecco come crearle

D3DXMatrixPerspectiveFovLH(&projection,angle,ratio,ZNear,ZFar);

D3DXMatrixPerspectiveFovRH(&projection,angle,ratio,ZNear,ZFar);

Con queste si creano prospettive (bisogna sempre far riferimento al sistema scelto). Angle è l’angolo della telecamera, ratio è la proporzione tra X ed Y (esempio 4/3 si usa per schermi le cui dimensioni stanno in proporzione 4 a 3). ZNear e ZFar sono la minima distanza e la massima distanza visibili sulla Z. Questo significa che un oggetto sarà visibile solo se si trova ad una distanza dal ViewAt compresa tra questi 2 intervalli.

D3DXMatrixOrthoLH(&matrix,width,height,ZNear,ZFar);

D3DXMatrixOrthoRH(&matrix,width,height,ZNear,ZFar);

Queste 2 invece servono per creare matrici ortogonali. Width ed Height sono la dimensione orizzontale e verticale che si vuole siano visibili sullo schermo.

Terminata la trasformazione avremo tutti gli oggetti visibili posizionati tra -1 ed 1 mentre saranno invisibili quelli fuori. La trasformazione tiene conto ovviamente anche della profondità. DirectX10 ritiene visibili tutti gli oggetti compresi tra 0 ed 1. Sarà infine la scheda video che posizionerà la scena compresa in questo intervallo affinché copra tutta l’area visibile sul monitor.

Le dimensioni degli oggetti non saranno in pixel, ma in “unità”, ossia semplicemente numeri. Cosa vedremo dipenderà dalle 3 matrici.

Moltiplicando le 3 matrici (world, view e projection) tra di loro otterremo la matrice Transformation che, come spiegato all’inizio, è la somma delle 3 trasformazioni. Ora prendiamo il nostro shader e creiamo una variabile matrice (che in HLSL è float4x4) e moltiplichiamola per la posizione in entrata.

struct VS_INPUT

{

    float4 Pos : POSITION;

    float4 color:COLOR;

};

struct PS_INPUT

{

    float4 Pos : SV_POSITION;

    float4 color:COLOR;

};

float4x4 transformMatrix;

PS_INPUT VS( VS_INPUT input )

{

    float4 v=float4(0,0,0,0);

    PS_INPUT output = (PS_INPUT)0;

    output.Pos = mul(input.Pos,transformMatrix);

    output.color=input.color;

    return output;

}

In questo modo la posizione di uscita sarà trasformata e sullo schermo vedremo il nostro oggetto muoversi rispettando le regole date. Consiglio di provare le matrici il più possibile in modo da comprenderne a pieno il funzionamento. Molto spesso se un oggetto non è visibile è un problema di matrice.

Vi lascio al demo

Demo