Il termine CAD, Computer Aided Design tradotto in italiano come Progettazione Assistita al Calcolatore è la disciplicana che prevede il disegno grazie all'utilizzo del computer. Il termine trova il suo pieno significato nel disegno tridimensionale e quindi nella rappresentazioni di oggetti ed ambienti virtuali. I videogames derivano dal CAD da cui però non ereditano tutte le possibilità in quanto a differenza dei programmi di grafica come 3DStudioMax i primi devono lavorare in real time ad alta velocità. Una delle caratteristiche usate in CAD e disponibile ormai anche su molte schede video sono le High Order Primitive, ossia delle curve geometriche. Tra queste rientrano molte curve che a volte sono state nominate senza spiegare cosa siano. Curve di Hermite, le BSpline, le ormai "leggendarie" curve di Bezier o le NURBS. Queste particolari curve altro non sono che curve dotate di grandi flessibilità che possono essere tracciate tramite pochissime informazioni e che possiedono numerose proprietà. Un esempio, sicuramente il più famoso, è la curva di Bezier che permette di tracciare una curva dati un punto iniziale e finale e 2 punti centrali che con quelli esterni ne stabiliscono la forma tramite tangente. Ecco un esempio di curva di Bezier (bianca) dati 4 punti (verdi).

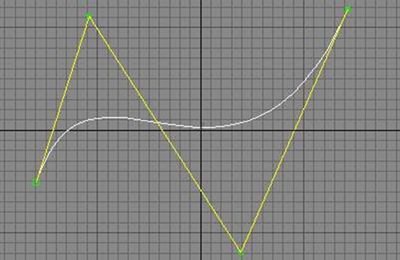
Esistono numerosi tipi di curve che derivano spesso le une dalle altre come ad esempio le BSpline che permettono di montare più curve di Bezier in seguenza o le NURBS in cui ad ogni punto è anche associato un peso che ne determina l'importanza per il tracciamento della curva. Le curve diventano superfici quando ai punti si sostituiscono altre curve. Le equazioni di queste curve sono inoltre indicate come gruppo di equazioni dette parametriche ossia per ogni componente X,Y,Z della curva esiste una equazione in una variabile generica (che chiameremo U) che variando ad esempio da 0 a 1 genera la curva (per le superfici c'è ne sono 2 essendo curve di curve). Al di là delle complicatissime implicazioni matematiche racchiuse nei calcoli di queste curve e superfici esistono degli aspetti che le rendono adattissime per la computer grafica

1. sono sufficienti pochi punti o poche informazioni per tracciare una curva di grande flessibilità (4 punti per una curva simile invece dell'intera seguenza di punti di cui è composta)
2. Variando opportunamente la variabile U (e V per le superfici), possiamo approssimare la curva ad una seguenza di sezioni rettangoli e quindi di triangoli adatte alle directX
3. Ruotando, traslando o scalando i punti le curve mantengono le loro caratteristiche

Per questi motivi le suddette curve sono ampiamente usate in molti settori industriali a partire da quello automobilistico in cui sono nate (Bezier lavorava come ricercatore automobilistico alla renault nel 1966)

Perchè sono importanti per i nostri scopi? Semplice:

Se per disegnare questa curva abbiamo dovuto usare solo 4 punti invece della serie di segmenti allora possiamo inviare solo questi punti alla scheda video. Il risultato di tutto ciò sono le High Order Primitive, superfici che si creano a partire da pochi punti dati e che possono diventare più o meno dettagliate (ossia formate da più o meno triangoli) variando in modo dinamico il valore di segmentazione delle linee. La superficie diverrà quindi sempre più morbida ma le prestazioni della scheda video verranno intaccate in misura molto minore dato che non saremo noi a passare un gran numero di triangoli ma sarà la scheda a generarli. Il risultato è:

1. Diminuzione significativa dello scambio di dati tra le memorie di sistema (ad esempio una superficie di 100000 poligoni con soli 100 punti)
2. Miglioramento delle prestazioni
3. Fluidità delle superfici

Dato che tutti i modelli 3D possono essere implementati con curve di questo tipo capite bene gli incredibili vantaggi di questa tecnologia.

DirectX9 supporta le high order primitive in numerosi modi. Quelli che tratterò sono le RTPatches e le NPatches. Queste ultime notevolmente più interessanti e semplici da usare. In questo tutorial saranno trattate anche le enchanted mesh.

RTPatches

Le RTPatches sono 2 modalità di rendering di primitive che anzichè utilizzare i triangoli utilizzano patch rettangolari e triangolari (rectangle-triangle patches). Innanzitutto visto che moltissime schede non supportano l'accellerazione hardware controllate il supporto tramite enumerazione

Dim c As Caps
c = Manager.GetDeviceCaps(0, DeviceType.Hardware)
DeviceCaps.SupportsRtPatches

Se supportRtPatches è uguale a true allora il supporto è assicurato altrimenti dovrete provare il ref mode.

Tratterò le patch rettangolari perchè sono più semplici e più interessanti. Le patch triangolari si utilizzano in maniera simile.

Dim rectP As new RectanglePatchInformation

Questo oggetto contiene le informazioni per il rendering di patch triangolari.

rectP = New RectanglePatchInformation
rectP.BasisType = BasisType.Bezier
rectP.Degree = DegreeType.Cubic
rectP.Width = 4
rectP.Height = 4
rectP.Stride = 5
rectP.StartVertexOffsetHeight = 0
rectP.StartVertexOffsetWidth = 1

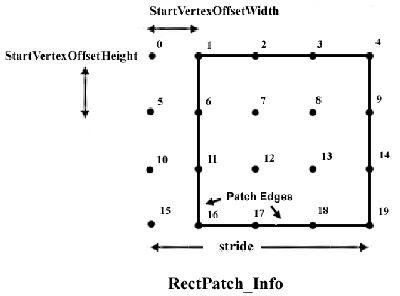
I vertici vengono disposti ordinatamente da sinistra a destra e dall'alto in basso in modo da formare una griglia (non necessariamente allineata su nessun asse). Ad esempio nella foto sono stati creati 20 vertici, da 0 a 19.

Questo è un esempio di settaggio. Le opzioni width e height sono la larghezza e l'altezza del rettangolo mentre stride è la lunghezza della riga totale usata per andare a capo (il rettangolo in foto è 4x4 ed ogni riga ha 5 vertici). StartVertexOffset sono invece i la posizione X e Y da cui iniziare il rettangolo. Come vedete il concetto di triangolo è completamente sparito.

I punti altro non sono che il nostro array inserito in un vertex buffer.

vb = New VertexBuffer(device, 32 * 256, Usage.RTPatches, VertexFormats.Position Or VertexFormats.Normal Or VertexFormats.Texture0, Pool.Default)

Notare l'usage RTPaches che ho usato. Lo si riempie con i dati e lo si invia al device.

device.VertexDeclaration = standardVertexD()
device.SetStreamSource(0, vb, 0, 32)

Ed infine utilizzare l'istruzione

device.DrawRectanglePatch(0, New Single() {numT, numT, numT, numT}, rectP)

Le variabili numT sono appunto la "tessellazione" della patch ossia la suddivisione effettiva della zona. Ad esempio con 1 si vedrà solo un quadrato ed aumentando i quadrati visibili saranno sempre di più e la curva inizierà a curvarsi sempre più morbidamente per seguire i punti dati. Ci sono 3 tipi di curve e 4 tipi di gradi. PEr il grado useremo il cubico (equazione di terzo grado). Per quelle di grado inferiore o superiore è sufficiente prendere zone più grandi per una patch.

Bezier

rectP.BasisType = BasisType.Bezier

Per il tracciamento delle patch di Bezier cubiche si devono prendere zone di 4 x 4 vertici. Per disegnare una grande superficie bisogna disegnare in seguenza tutti le patch affiancandole.

For j = 0 To  12 Step 3
    For i = 0 To  12 Step 3
        rectP = New RectanglePatchInformation
        rectP.BasisType = BasisType.Bezier
        rectP.Degree = DegreeType.Cubic
        rectP.Width = 4
        rectP.Height = 4
        rectP.Stride = 16
        rectP.StartVertexOffsetHeight = j
        rectP.StartVertexOffsetWidth = i
        device.DrawRectanglePatch(0, New Single() {numT, numT, numT, numT}, rectP)
    Next
Next

In questo esempio la patch ha dimensioni 16 x 16.

BSpline e CatMullRom

Le BSpline e le catMullRom hanno molta liberà perchè possono essere tracciate non necessariamente in patch di 4 x 4 ma anche a comprendere l'intera zona come un unico rettangolo. Il risultato è che all'aumentare dei segmenti la patch inizierà a considerare i punti intermedi e a prendere la sua forma.

rectP = New RectanglePatchInformation
rectP.BasisType = BasisType.BSpline
rectP.Degree = DegreeType.Cubic
rectP.Width = 16
rectP.Height = 16
rectP.Stride = 16
rectP.StartVertexOffsetHeight = 0
rectP.StartVertexOffsetWidth = 0
device.DrawRectanglePatch(0, New Single() {numT, numT, numT, numT}, rectP)

Le 2 curve si differenziano per il tipo di curva anche se non sono molto dissimili.

Per le patch triangolari il processo è simile ovviamente i segmenti usati sono 3 e si usano le trianglePatchInformation ed il drawTrianglePatch.

Come vedete la struttura di posizionamento dei vertici è in questo caso a piramide.

NPatches

Le npatches sono patch automatiche che possono essere adoperate senza troppi trattamenti. La semplicità è addirittura spiazzante:

Create la mesh con opzione MeshFlags.Managed Or MeshFlags.Use32Bit or MeshFlags.NPatches. Il secondo flags serve per utilizzare indici a 32bit (se 16 bit permettono di considerare fino a 65536 vertici con le 32 arriviamo a 2^32, valori che possono essere raggiunti). L'opzione NPatches sembra essere inutile, forse a causa della scheda video in mio possesso. Ora non vi resta che aumentare il valore di:

device.NPatchMode

Il risultato sarà simile a quello delle RTPatches ma le curve saranno molto più morbide. A seconda della scheda video questo processo sarà più o meno veloce (potete controllare il supporto NPatches). Non è possibile aumentare all'infinito ed oltre un certo limite la mesh smette di aumentare il numero dei suoi poligoni.

Notare che il numero di poligoni non aumenta realmente nella mesh ma solo a livello di rendering.

Enchanted mesh

Questo non è un vero tipo di mesh ma semplicemente un processo che aumenta i vertici come le Npatches. Questo può essere fatto all'infinito e anche in questo caso a seconda dei sistemi si può vedere un incremento delle prestazione. Create una mesh

meshP = Mesh.FromFile(fileSrc, MeshFlags.Managed Or MeshFlags.Use32Bit or MeshFlags.NPatches, device, adia, materiali)

dove adia è un graphicsStream. Conservate la mesh ed il graphics stream che contiene le adiacency ovvero i triangoli vicini ad ogni triangolo.

mesh = Mesh.TessellateNPatches(meshP, .adia, numSegs, False)

Dalla meshP generate la mesh suddivisa in segmenti. Conservate sempre la mesh principale perchè è meglio partire da lei per creare la mesh tessellata. Qui i vertici aumentano realmente e quindi potete verificare direttamente i triangoli visualizzati.

Vi lascio 2 esempi, il primo che renderizza RTPatches ed il secondo che mostra nPaches e Enchanted Mesh al lavoro.

Esempio VB.Net - Patch

Esempio VB.Net - NPatch