Uno dei problemi che si possono incontrare quando si comincia a lavorare in 3D è spesso la gestione stessa degli ambienti tridimensionali. Infatti, a differenza dei giochi bidimensionali, occorre avere una buona matematica per fare in modo che tutto sia visualizzato correttamente. I principi teorici su cui si fonda la grafica a 3 dimensioni sono infatti molto complessi e spesso oggetto solo di corsi universitari e professionali. In grafica 3D movimenti, rotazioni, ridimensionamenti sono comunemente chiamati trasformazioni geometriche e non è sufficiente dire "spostati a destra o ruota" perchè i dettagli sono molti. Trasformare un solido significa eseguire delle operazioni su ogni vertice in modo che il poligoni venga trasformato in modo corretto. L'operazione da applicare è un prodotto di ogni singolo punto per una matrice. Le matrici sono griglie di numeri (per la grafica 3D di dimensioni 4x4) che possiedono numerose proprietà. Per spostare un oggetto di tre posizioni si moltiplica ogni vertice per una matrice di traslazione. La cosa più interessante è che si moltiplica per quel vertice il prodotto di una matrice di traslazione con una di rotazione i due movimenti verranno inseriti in seguenza ma attenzione all'ordine:
TRASLARE e RUOTARE è DIFFERENTE DA RUOTARE E TRASLARE, guardate sotto.

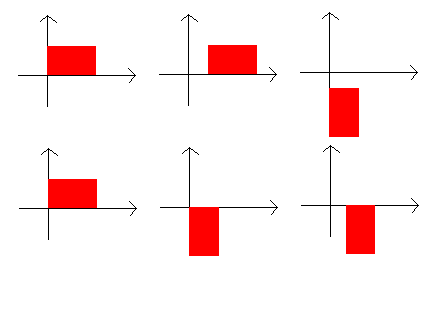
In alto ho applicato prima una traslazione a destra e poi una rotazione di 90° in senso orazio. Sotto ho invece applicato prima la rotazione e poi la traslazione e come potete vedere la situazione è diversa. Questo perchè le trasformazioni vengono sempre fatte considerando come centro l'origine degli assi e perchè il prodotto di matrici non è commutativo.
Le matrici principali per le trasformazioni sono queste cinque qui sotto:

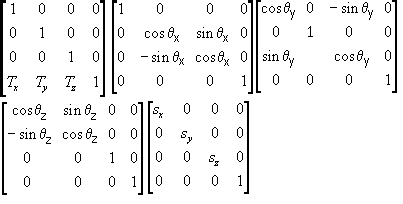
In ordine da destra a sinistra sono: la matrice di traslazione, le rotazioni X, Y, Z e quella di ridimensionamento. Per disegnare un oggetto occorre moltiplicare tra di loro le varie matrici a secondo del movimento e successivamente moltiplicarle per tutti i vertici.

Per programmare Direct3D devo sapere tutto questo?

Solo in teoria per le cose più semplice. In realtà è Direct3D che fa tutte queste cose: noi dobbiamo solo eseguire le varie operazioni matriciali tramite dei generatori della classe Matrix e passarle al device prima di ogni rendering degli oggetti.
La classe Matrix contiene in memoria una matrice 4x4 ed è sufficiente dichiararla:

Dim m As Matrix()

La classe Matrix esegue la moltiplicazione (e qui devo dire in maniera molto migliore rispetto a DirectX8).

Matrix.Multiply(m2, m1)

ad esempio moltiplica m2 x m1 (due matrice) e restituisce la matrice prodotto tra le due. Per chi ha usato DirectX8 l'operazione restituiva un riferimento. Non serve quindi memorizzarla ma è possibile passarla direttamente al device

device.Transform.World = Matrix.Multiply(m2, m1)

Potete anche non usare alcun oggetto matrice dato che i metodi che andremo ad usare sono della classe Matrix e tutti restituiscono un risultato (ma concatenare tutto può risultare ostico se non state attenti).
Ecco come creare le trasformazioni elementari.

Traslazione

matrix.Translation

Riceve come argomenti o un Vector3 da riempire con il numero di unità di cui si vuole spostare l'oggetto o direttamente 3 single X, Y, Z. Dato che molti ci cascano lo ripeto.
La matrice traslazione non dice la posizione: ma di quanto ci si sposta. Se si moltiplicano 2 matrici traslazione una con X=+3 e una con X=-2 l'oggetto andrà sulla X prima di 3 e poi tornerà indietro di 2. Tutti i punti saranno spostati sulla X di 1. Ciò non significa che l'oggetto si troverà necessariamente nel punto con X=1. Se l'oggetto non è stato creato al centro oppure sono state fatte prima altre trasformazioni dovrete fare i conti con la nuova posizione (riguardate il disegno).
Rotazione elementare

Matrix.RotationX (angolo)
Matrix.RotationY (angolo)
Matrix.RotationZ (angolo)

Ruota l'oggetto intorno all'asse specificata (non il centro dell'oggetto ma l'asse cartesiano).
Le rotazioni sono la cosa più complicata da concatenare percè se non vi fermate a riflettere un attimo le cose vi sembreranno molto strane. Se l'oggetto deve ruotare su se stesso fate in modo che si trovi al centro prima di effettuare la rotazione altrimenti vi succederà lo scherzo della trasformazione del disegno. In genere se l'oggetto è stato disegnato al centro allora le rotazioni dovrebbero essere le prime matrici nella moltiplicazioni. Notate infine che gli angoli sono in radianti (moltiplicare l'angolo in gradi per il valore di pi greco/180 (per i profani circa 3.14 o per avere il valore più preciso viene restituito da VB tramite math.pi).
Scala Matrix.Scaling Come argomenti riceve o un vector3 o le tre proporzioni X,Y,Z. Con 1 l'oggetto è a grandezza standard, con 2 diventa il doppio mentre con 1/2 la metà.
Il ridimensionamento non fa altro che rimpicciolire o ingrandire l'oggetto sempre rispetto all'origine degli assi. Di conseguenza se volete che l'oggetto sia effettivamente rimpicciolito dovrete inserire la matrice di scala ancora prima di quella di rotazione o comunque quando l'oggetto si trova al centro. Pena guardate l'immagine in cui viene fatta una scala quando l'oggetto non si trova al centro (seguenza in basso):

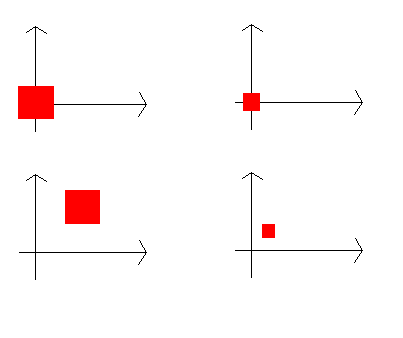
Come vedete l'oggetto viene rimpicciolito ma viene spostato verso il centro (quindi non va bene per applicare altre trasformazioni).

Esempio completo.

Voglio che l'oggetto venga prima ruotato sull'asse Z di 90°, poi ruotato sull'asse X di 35 ed infine traslato.

m1 = Matrix.Translation(2,0,3)
m2 = Matrix.RotationZ(90 * rad)
m3 = Matrix.RotationX(35 * rad)

Creo le matrici che fanno le trasformazioni. Poi le moltiplico.
m4=Matrix.Multiply(m2,m3) 'ora se passiamo la matrice al device farà prima la rotazione Z di 90 e poi la X di 35.
m5=Matrix.Multiply(m4,m1) 'ora la matrice contiene anche la traslazione finale

device.Transform.World= m5

Ora il prossimo oggetto che verrà renderizzato conterrà effettuerà le tre trasformazioni in seguenza.
Se poi volete usare meno matrici la stessa cosa può essere concatenata.

device.Transform.World = Matrix.Multiply(Matrix.Multiply(m2,m3),m1)

Fate come preferite. Se poi volete usare ancora meno variabili potete inserire direttamente le istruzioni generatrici.

Matrici speciali

Esistono alcune matrici che eseguono delle trasformazioni particolari che possono essere usate solo su matrici già pronte (quindi all'oggetto ad esempio m1 e non alla classe).

m1.Shadow(luce, piano)

In questo modo la matrice precedentemente preparata diventerà un 'ombra (nel senso che l'oggetto sarà schiacciato su di un piano).
La luce è un vector4.
Se usate la luce puntiforme dovete porre X,Y,Z uguali alla posizione della luce e porre w=1 mentre per la luce direzionale X,Y e Z devono essere l'opposto della direzione (così come avete impostato nel device la direction) e porre W=0.
Il piano è un oggetto plane (che rappresenta l'equazione del piano ax+by+cz+d). Se siete bravi in matematica potete impostarlo da soli ma è più comodi crearlo così
piano=plane.FromPoints(p1,p2,p3) 'piano passante per 3 punti p1,p2,p3 (i punti sono rappresentati da vector3).
L'oggetto sarà schiacciato su quel piano (il piano ovviamente non si vede). L'ombra comunque non è reale perchè non copre gli oggetti e non si curva. L'unica cosa che potete fare è usare un materiale nero e renderizzarlo. L'effetto è comunque ottimo:

Riflessione

Per la riflessione è sufficiente passare il piano rispetto al quale l'oggetto verrà riflesso

m1.Reflect(piano)

Attenzione però che verrà invertito anche il verso dei triangoli (ricordate i primi tutorial?). Andate all'effetto Cull mode della sezione effetti vari.

Trasformazioni composte

Esistono anche delle istruzioni nella classe Matrix (le avrete viste) che eseguono in un solo colpo molte trasformazioni elenchiamole.

Rotazione su un asse

Matrix.RotationAxis(asse, angolo)

Effettua una rotazione su un asse (vector3). Le componenti X,Y,Z si calcolano come punto finale - punto iniziale. L'asse passante per i punti (1,2,3) e (4,5,6) è (4-1,5-2,6-3)= (3,3,3)

Identità

Matrix.Identity

Restituisce l'elemento neutro della matrice. Moltiplicare una matrice per l'identità o viceversa non cambia il valore della matrice (come l'1 nella moltiplicazione). Molto utile perchè se la passate al device significa posizionare l'oggetto nella sua posizione base.
Altre istruzioni fanno uso di altri oggetti o sono dedicati alle telecamere e alla proiezioni. Imparare ad usare le trasformazioni è la cosa più importante. Fate moltissime prove e capirete il meccanismo (dopo di che è fatta).