Durante il nostro percorso in DirectX, ci ritroveremo sicuramente ad avere a che fare con le luci, elemento importantissimo.
Dato che l’unico modo per rappresentare queste ultime in realtime è “sottoforma di equazioni”, in cui entrano in gioco vettori, normali, operazione di normalizzazione, è forse il caso di fare un po’ d’ordine.
Cercherò quindi di guidarvi attraverso la luce seguendo i modelli di riflessione di Lambert e Phong, definendo eventuali operazioni vettoriali di cui avremo bisogno.
Il primo dubbio che viene a qualsiasi persona è (credo) “Come può un vettore essere rappresentato tramite un solo punto?”
In effetti, in DirectX i vettori sono generalmente associati alla struttura D3DVECTOR (e le sue estensioni D3DXVECTOR2, 3, 4), che contengono componenti x,y,z,w a seconda del numero di elementi.
Per individuare un vettore non basta un punto, ma abbiamo bisogno di direzione, verso e modulo.
La direzione è la retta sulla quale giace il segmento del vettore. Sapendo che una retta è individuata da 2 punti, e che nella struttura D3DVECTOR ne abbiamo soltanto 1, qual è il secondo punto? E’ sempre l’origine degli assi: il punto O(0,0,0).
Avendo sempre questo punto di riferimento, grazie al secondo da noi scelto, abbiamo il nostro vettore (o meglio, la direzione del nostro vettore)
D3DVECTOR in effetti è una struttura che può definire sia un punto che un vettore, a seconda di come sia da voi interpretato. La differenza sostanziale è questa

Se stiamo considerando la struttura come un punto, allora indicherà il punto A, se come vettore, allora prenderemo in considerazione anche il punto dell’origine, per avere il vettore.
Domanda spontanea…quando è che considero la struttura come un punto e quando come un vettore?
Bhè è a seconda dei casi: se per esempio abbiamo intenzione di disegnare una serie di punti sullo schermo, DirectX (sapendo che volete disegnare dei punti) utilizzerà la struttura come un punto.
Se invece ci accingiamo a fare operazione di “illuminazione”, allora userà la struttura come un vettore.
Questo era nella fixed pipeline. Essendo ora la pipeline completamente programmabile, DirectX non fa niente, saremo noi, nei nostri shaders, a fare l’uso appropriato dei dati che ci arrivano.
C’è però un altro caso da ricordare: se voglio creare un vettore che non abbia come punto di origine il punto O (origine degli assi), come devo fare?
Prima cosa diciamo che il punto O (origine degli assi) si chiama punto di applicazione del vettore. E’, molto volgarmente, il punto da cui parte il segmento che descrive il suo modulo.
Ad ogni modo, sappiamo che un vettore può essere rappresentato come la differenza tra 2 punti in cui questo passa. Questa regola d’oro ci permette di calcolare qualsiasi vettore, facendo una semplice differenza tra 2 punti.
In effetti, qualsiasi vettore facciamo, non è altro che una differenza tra il punto definito nella struttura e l’origine degli assi, che ha coordinate 0,0,0.
Se abbiamo il punto A(1,1,1) e il punto B(2,3,4), il vettore passante per i 2 punti sarà (2-1,3-1,4-1) = (1,2,3).
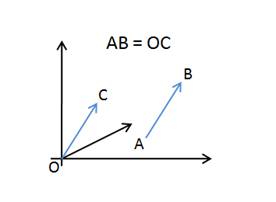
Un’altra cosa da ricordare: il vettore appena ottenuto, in fondo, è equivalente al vettore passante per il punto 0,0,0 e 1,2,3.
E’ un vettore equivalente, con direzione parallela a quella data, stesso modulo e verso.
Perciò ogni vettore che creiamo alla fine si riduce a un vettore passante per l’origine degli assi.
Diciamo che ora piu’ o meno la direzione l’abbiamo capita. Ci rimane modulo e verso.
Il modulo è una grandezza scalare associata al vettore (scerifficamente, è la lunghezza del vettore). Questo può essere calcolato tramite le funzioni D3DX associate (D3DXVec3Length), o tramite la funzione HLSL length.
Come funziona quest’ultima? Non sarebbe oggetto di tutorial, ma comunque, per il teorema di Pitagora, la somma dei quadrati costruito sui cateti è uguale al quadrato dell’ipotenusa.
Ogni vettore, in uno spazio monometrico ortogonale, è un ipotenusa di un ipotetico triangolo rettangolo.

Adesso abbiamo capito anche il modulo.
Il verso. Da cosa dipende il verso? Bella domanda: non lo so.
Passiamo ad’un’altra operazione importante che si compie sui vettori: la normalizzazione. Cosa significa normalizzare, e perché si normalizza?
La Normalizzazione in consiste nel dividere tutti i termini di un'espressione per uno stesso fattore.
In pratica significa fare sì che il suo modulo sia 1, preservando l'orientazione. Insomma, un vettore normalizzato è di fatto un versore (che è un vettore avente modulo unitario).
Perchè si normalizza un vettore? A cosa serve?
Perchè a volte è più comodo avere un vettore normalizzato, che indica solo la direzione e non ha "attributi propri".
Serve, insomma, ad indicare soltanto una direzione.
Le funzioni che eseguono questa operazione sono D3DXVec3Normalize o normalize da HLSL.
Le operazioni da eseguire per normalizzare un vettore sono le seguenti:
· - Calcolare la lunghezza del vettore (vedi sopra)
· - Dividere ogni componente del vettore per la lunghezza appena calcolata.

E adesso passiamo effettivamente alla luce.
Cominciamo con il modello di riflessione di Lambert (matematico francese).
Prima però di cominciare a programmare sarebbe bene capire cosa dice il modello di riflessione di Lambert:
“Se un oggetto viene esposto al modello di riflessione di Lambert, la luce che cade su quest’ultimo si sparge come l’apparente brillantezza della superficie che quest’ultima avrebbe con una direzione fissa della luce.”
Praticamente, questo modello di riflessione è isotropico (ossia uguale da tutte le parti).
La legge dice in poche parole che la luce che si riflette è uguale in tutti i punti.
E’ necessario calcolare quindi questa luce uguale a tutti i punti: dalla legge possiamo facilmente notare che la luce varia in base all’angolo dell’osservatore.
Dunque la luce è direttamente proporzionale all’angolo formato dalla luce e l’oggetto che stiamo vedendo.
Ovviamente però, non tutti gli oggetti reagiscono allo stesso modo con una luce. Ogni oggetto ha le sue caratteristiche (il legno, il ferro…ognuno riflette la luce ad ogni modo).
Per simulare le caratteristiche dei materiali si usano apposite strutture (chiamate proprio materiali), che contengono i 4 colori: in base a queste si avrà l’effetto desiderato.
Ricapitolando, abbiamo che

In parole:
La luce riflessa è uguale al prodotto tra il vettore normalizzato della direzione della luce (L), le normali (normalizzate) del punto, il colore della luce e l’intensità della luce.
A questa equazione va aggiunto un * M (M è il materiale dell’oggetto).
Le normali sono già normalizzate (lo dice stesso il nome.).
Dunque non c’è bisogno di effettuare su di loro l’operazione normalize
Giusto per conoscenza, l’unico materiale che rispetta per davvero questo modello di riflessione è lo Spectralon.
Eseguiamo allora questa operazione in HLSL.
float4 ps_main(PS_INPUT In) : SV_TARGET
{
float3 L = normalize(DirezioneLuce.xyz);
float4 D = saturate( dot(In.Nor,L) * ColoreLuce * MaterialColor);
return D;
}
Una volta compilato il tutto, e caricata la scena, ecco il nostro risultato

Come potete vedere una luce abbastanza anonima, ma buona per illuminare i primi oggetti.
E’ possibile aggiungere, alla formula, un prodotto con un float chiamato attenuazione, per decidere la potenza della luce.
Cerchiamo ora di passare da Lambert a Phong.
Il modello di riflessione Phong è una versione evoluta del modello di Lambert.
Alla luce diffusa aggiunge, infatti, il componente speculare.
Sebbene abbia circa 25 anni ed esistano oramai vari modelli alternativi piu’ o meno realistici, continua ad essere il piu’ diffuso.
E’ semplice e sufficientemente realistico in molte applicazioni.
La principale differenza dal modello diffuso consiste nel fatto che l’aspetto visivo della riflessione dipende dalla posizione dell’osservatore. Quando la direzione dell’osservatore coincide o si avvicina a quella del raggio riflesso, viene osservata una chiazza luminosa, chiamata in gergo specular highlight. Tutto ciò simula la riflessione della luce da parte di superfici molto levigate come ad esempio quelle metalliche. Il modello matematico per questo tipo di riflessione è stato creato da Phong Bui Tong e dipende da: direzione della luce L, posizione dell’osservatore V, direzione normale alla superficie N, direzione della luce riflessa R
Alla luce delle conoscenze acquisite nel tutorial, implementiamo il modello Phong
float4 ps_main(PS_INPUT In) : SV_TARGET
{
float3 L = normalize(LightDirection.xyz);
float4 D = saturate(dot(In.Nor,L) * ColoreLuce) * MaterialColor);
float3 V = normalize(EyePosition - In.WorldPos);
float3 R = normalize(2.0F * In.Nor * dot(In.Nor,L) - L);
float4 S = pow(max(0.0F,dot(R,V)),PotenzaLuce);
return D + S; //Lambertian + SpeculareDiPhong
}
Per prima cosa calcolato il modello di riflessione Lambertiano D
Dopo di chè abbiamo trovato la posizione dell’osservatore V
Abbiamo cercato la direzione della luce riflessa R (ricordate: PuntoA – PuntoB)
Calcolato la componente speculare S.
Ritorno D + S

Con questo si conclude il tutorial,
spero di essere stato utile a capire qualcosa in piu’
Niente demo per voi stavolta, provateci da soli!!!
Vincenzo Chianese
http://xvincentx.netsons.org/programBlog